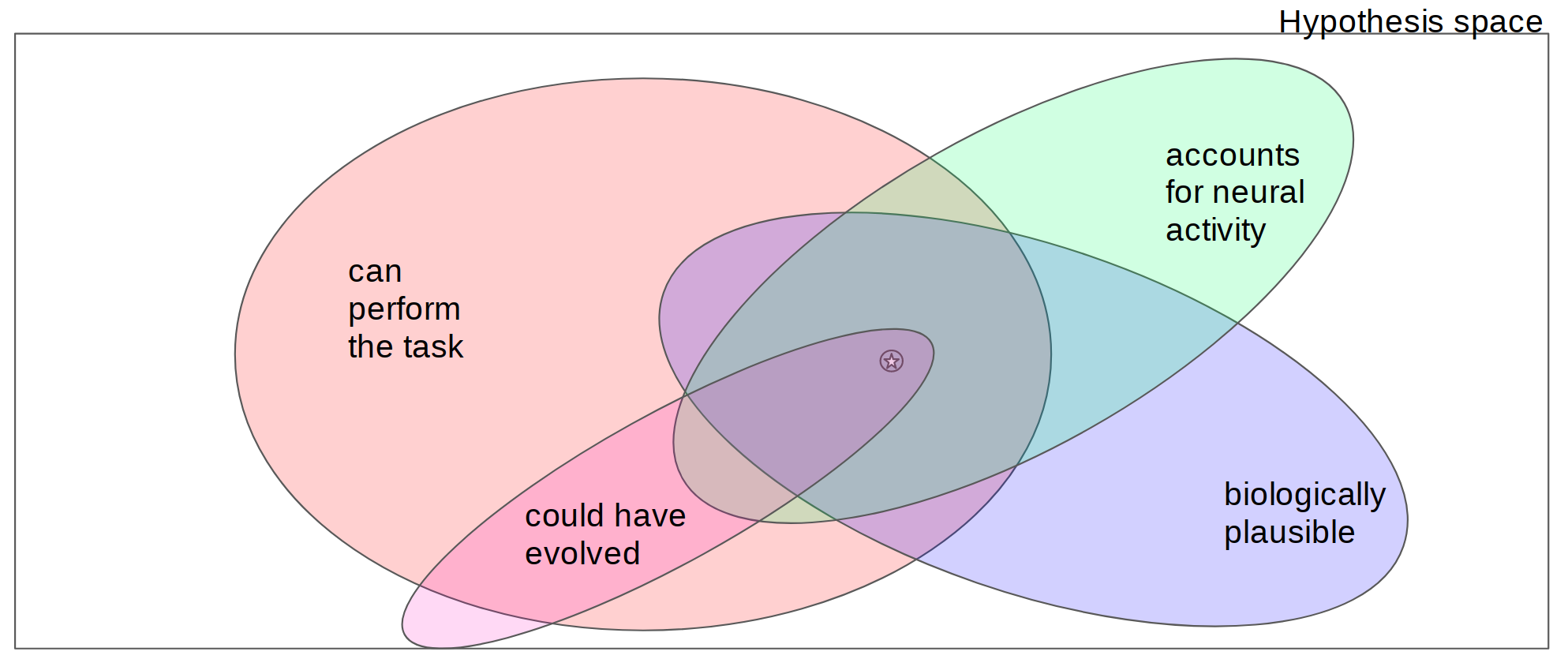
Model Comparison Hypothesis Space Figure 1. Models lie at the intersection of one or more constraints. The rectangle indicates the space of all possible models where each point in the space represents a different model of some phenomenon. Regions within the coloured ovals correspond to models that satisfy specific specific model constraints (where satisfaction could be defined as passing some threshold of a continuous value). If a constraint is well-justified, this implies that the true model is contained within the set of models that satisfy that constraint. Models that meet more constraints, then, are more likely to live within a smaller region of the hypothesis space and hence will be closer to the truth, indicated by the star in this diagram.

The following is a lightly edited excerpt from the Discussion chapter of my doctoral dissertation which was successfully defended on Nov 20, 2020.

On using deep neural networks as models of sensory systems

The use of DNNs as models of animal sensory systems is largely in the context of a model comparison approach to scientific discovery. Through evaluation, comparison, and iterative refinement, models hopefully get closer to some truth about the phenomena under study (or at least the models become more useful, if one prefers a more pragmatic, less realist account). Within this view, models that are more constrained are likely to be closer to the truth since they occupy smaller region of the search space known to include the true model (Fig 1). In practice, however, a priori we don’t usually know which constraints are necessary to answer a specific scientific question or how a particular set of constraints will affect our exploration of the hypothesis space.

The use of DNNs as models of sensory systems emphasizes a different subset of constraints than alternative modeling approaches. For example, Kell and McDermott (2019) discuss the importance of task constraints and of models that exhibit the phenomenon to be explained. For example, if one wants to study face recognition, a reasonable possible model constraint is that the model be capable of recognizing faces. Emphasizing task-performance and accounting for animal behaviour may come at the expense of other possible model constraints since it is usually impossible to satisfy all model constraints at once.

The various differences between DNNs and biological brains are often repeated to refute their usefulness as models. In particular, the biological (im)plausibility of DNN models and their limited ability to replicate high-level cognition are often cited. Marcus (2018) describes the limitations of current DNNs. They are not capable of relational reasoning, cannot accommodate non-stationarity, do not extrapolate well, and cannot separate correlation from causation, among other limitations that human brains have managed to overcome. Zador (2019) questions the relevance of models that required large datasets to learn when most animal behaviour is the result of eons of evolution and encoded in the genome rather than learned over the course of a lifetime. DNNs and animals fail in different ways. DNNs are susceptible to adversarial examples—examples that have been only slightly modified such that the differences are not noticeable by humans, but can severely affect the performance of a network (Goodfellow et al., 2015). Since DNNs are only loosely inspired by biological neural networks, there are enumerable physiological details that are missing. Biological plausibility has been presented as a requirement for models to be useful for studying biological neural computation (Gerven and Bohte, 2017) and the biological plausibility of learning in DNNs has been questioned. There are many differences between DNNs and biological brains, but what do they imply about how we ought to think about DNNs as models? Why are these differences meaningful?

Criticisms of the use of DNNs as models of sensory systems often amount to claims that a different subset of constraints should be privileged. The proposed requirement that models must be biologically plausible in order to have bearing on neuroscience prioritizes the purple region of Figure 1 which contains only models that are deemed biologically plausible. According to the view put forth by Love (2019), positions of this type reflect value judgements about which datasets are most important. On what basis are such value judgements made? Within the model comparison framework, constraints (or datasets) are selected to narrow the search space. Constraints could be privileged based on how much they narrow the search space. However, when comparing two constraints like biological plausibility and task performance, it is not obvious that one will narrow the search space more than the other. It is entirely possible that exploring the space of possible models that can perform some task of interest will lead to truth faster than exploring the set of models that are biologically plausible. These known unknowns can inform how we think about optimizing scientific progress in a model comparison framework.

We can try to reason about which constraints are more limiting and it may be more or less possible for different research questions. In Article 1, I emphasized the importance of specifying the phenomenon to be explained. Similarly, Love (2019) emphases a similar need to identify the datasets to be accounted for. Different researchers, even researchers who are concerned with the same natural phenomenon, may still choose to privilege different model constraints and this is a feature, not a bug. Due to our uncertainty about the nature of the hypothesis space to be explored, we need different researchers to come at the same problem from as many different angles as possible. This has been studied using simulations of scientific discovery in a model-centric framework to identify the relationship between several attributes of scientific communities and the success of their research program. Devezer et al. (2019) found that innovative research speeds up the discovery of scientific truth by facilitating the exploration of model space and that epistemic diversity, the use of several research strategies, optimizes scientific discovery by protecting against ineffective research strategies. The authors compare epistemic diversity to diversifying an investment portfolio to reduce risk while trying to optimize returns. If one knew how the market was going to change, one wouldn’t need a diverse investment portfolio. Similarly, uncertainty about scientific truth and how to search for it should lead us to embrace epistemic diversity.

The long list of differences between DNNs and brains has no general implication for the suitability of DNNs as models of biological intelligence and learning. Specific differences may be relevant to specific research questions. Nevertheless, researchers are currently working on addressing several of these differences to further narrow the model search space. Machine learning researchers are currently working on biologically plausible learning algorithms (Bengio et al., 2014; Lillicrap et al., 2014; Guerguiev et al., 2017), relational reasoning (Bahdanau et al., 2018; Santoro et al., 2017), and causal inference (Schölkopf, 2019; Goyal et al., 2019). Neuro-AI researchers have been exploring the effects of adding elements of biological realism to DNNs to see how they affect representational correspondence (Lindsay and Miller, 2018; Lindsay et al., 2019). Storrs and Kriegeskorte (2020) hypothesize that, as the field of deep learning continues to progress, neural network models will only become more relevant and useful for cognitive neuroscience. They discuss how the study of relational reasoning in artificial systems helps to identify the necessary and sufficient conditions for such abilities to develop and how artificial systems trained in simulated environments can be used as a tool for studying embodied cognition. The use of DNNs as models of biological neural system is one of several well-justified modeling approaches. DNN models focus on different regions of model space than alternative approaches, and thus constitute an innovative strategy that increases the epistemic diversity of computational neuroscience.

Unifying Neuroscience and AI: Disambiguating prediction, representation and explanation

Many terms are used in different ways at the intersection of neuroscience, AI and philosophy of science. An integration of neuroscience and AI will require a consistent language. Here, I try to map between related concepts in cognitive science, statistics and machine learning.

Representation and encoding

Much effort has been directed at representations and their role in cognition and explanation. Marr and Nishihara (1978) defines a representation as “a formal system for making explicit certain entities or types of information, together with a specification of how the system does this.” He denotes a specific instance of an entity in a given representational system as a description. For example, the Arabic numeral 37 is a description of the number 37 that makes explicit its decomposition into powers of ten. A binary representation of the same number would make explicit its decomposition into powers of two. A representation will often be a useful abstraction. For example, we can represent strands of DNA as sequences of nucleotides, represented by the letters A, T, C and G. Similarly, the information processing approach to cognitive neuroscience presumes that the brain is likely to use various representations of sensory information at different stages along some pathway to facilitate certain computations. The terms encoding and decoding refer to representational transformations from the sensory input (encoding) and to perception or behaviour (decoding). According to Diedrichsen and Kriegeskorte (2017), information-based analyses of neural measurements (encoding analysis, decoding analysis, representational similarity analysis, etc.) test representational models, which describe how patterns of activity relate to sensory stimuli, motor actions, or cognitive processes. Their definition of representation within this framework is that a represented variable can be linearly decoded from a down-stream area. This paradigm, sometimes referred to as neural coding, has led researchers to make statements about what is ’encoded’ in neural signals based on the results of encoding and decoding analyses.

This paradigm has received criticisms on several fronts. Brette (2019) points out that the language of the neural coding framework implies causal relationships for which the analysis typically does not provide evidence. That the activity of a population of neurons can be well predicted by a particular representational model does not in itself imply that the hypothesized representation is in fact used by the neural system to accomplish the task of interest. Many candidate representational models may predict the relevant neural activity equally well. Using predictive performance as the only arbiter of model fit does not establish the causal relevance of the hypothesized representation. This debate reflects tensions between functional and causal mechanical theories of explanation. The neural coding paradigm en- tails the functional analysis of a neural system: decomposition of the component operations of a phenomenon. According to the functional theory of explanation, the causal mechanical implementation of those component operations are not needed. Although not stated explicitly, in essence, Brette’s warning regarding the interpretation of results in the neural coding paradigm reflect a warning against a functionalist view of explanation in neuroscience.

The neural coding paradigm has also received criticism from the dynamical camp. The dynamical hypothesis, is that ‘cognitive agents are dynamical systems’ (Gelder, 1998). The antirepresentational stance adopted by some dynamicists and radical embodied cognitive scientists claims that cognition is not inherently representational (Chemero, 2009): “Unlike digital computers, dynamical systems are not inherently representational. A small but influential contingent of dynamicists have found the notion of representation to be dispensable or even a hindrance for their particular purposes. Dynamics forms a powerful framework for developing models of cognition that sidestep representation altogether” (Gelder, 1998, 622). A dynamical explanation may make no reference to representation and instead describe the details of a particular neural circuit, for example.

The definition of representation in cognitive science and neuroscience is distinct from the notion of representation in machine learning. The field of representation learning is concerned with procedures for automatically learning useful transformations of data. The input data, say a set of images, are originally represented by a set of three-dimensional (RBG) pixel values. This pixel space is one representational space. Learned representations will consist of one or more transformations of this original form. In this sense, machine learning representations are representations of some signal whereas in cognitive science literature, a representation is a representation of some variable. In a DNN classifer, the target could be seen as a variable of interest. From the data processing inequality, we know that the mutual information with the target will be maximal at the input layer. All the information related to the target class is present at the input. The subsequent representational transformations change the form of that information, gradually linearizing the decision boundaries, such that the target class can be linearly read out at the output layer. One can add linear classifier probes at each layer of a deep network to see how well the target class can be decoded from each layer. For a trained network, one should see that the performance of these linear probes will increase with depth, but the decoding performance could be above chance at all depths (Alain and Bengio, 2016). In this case, where would the cognitive neuroscientist say the target is represented? At every layer? Or maybe at the input since that is where the mutual information is greatest? Or at the final layer since the decoding accuracy is highest there? From a machine learning perspective, what can be linearly decoded from a layer’s activity only provides a snapshot of its representational form.

Prediction, explanation, and generalization

In machine learning, the output of a model is a prediction. In classification, the prediction takes the form of a categorical label which represents the model’s best guess of the category of the input example. Traditionally, the goal of supervised machine learning is to discover statistical regularities and invariances in the training data that enable accurate predictions for a given task. The data are typically assumed to be independently and identically distributed (i.i.d); all observations are sampled independently from the same data generating process. The goal is a model with good generalization performance, which means that the predictions are accurate for any other sample from that data generating process. A model that overfits to the training data will not generalize well. For some models, there are analytic bounds on the generalization gap. In practice, this is typically verified empirically by separating datasets into training and testing sets. The performance on the test set estimates how well the model would predict any random sample from the same data generating process; this is referred to as within-distribution generalization. Some efforts in machine learning are focused instead on out-of-distribution generalization, which refers to the setting where the training and test sets are not i.i.d.

One example of out-of-distribution generalization is systematic generalization in language, which refers to the ability to rationalize about logical rather than purely statistical relationships between tokens. For example, (Bahdanau et al., 2018) investigated the ability ‘to reason about all possible object combinations despite being trained on a very small subset of them’:

Clearly, given known objects X, Y and a known relation R, a human can easily verify whether or not the objects X and Y are in relation R. Some instances of such queries are common in daily life (is there a cup on the table), some are extremely rare (is there a violin under the car), and some are unlikely but have similar, more likely counter-parts (is there grass on the frisbee vs is there a frisbee on the grass). Still, a person can easily answer these questions by understanding them as just the composition of the three separate concepts. Such compositional reasoning skills are clearly required for language understanding models.

Systematic generalization is something that is relatively easy for humans but difficult for artificial natural language understanding systems. Out-of-distribtion generalization also shows up in other applications. For example, one may wish to train a robotic arm first in a simulated environment controlled by a physics engine and want it to generalize to the real-world. Out-of-distribution generalization is one of the frontiers of AI research at the moment and will be required for AI systems to mimic human cognitive abilities. In this way, not all predictions are equal. Different predictions will test different generalizations.

In statistical hypothesis testing, commonly employed in the analysis of neural data, the word predict is employed in a different way. One variable is said to predict another if a significant statistical relationship has been found between the two. This use of the term is more akin to what philosophers call accommodation: how well a scientific theory accommodate the data that was already known at the time the scientific theory was constructed. When regression is used for statistical hypothesis testing, one variable (or set of variables or interaction of variables) is said to predict another based on an assessment of the experimental data. When using regression in machine learning, the model as a whole is predicting the target. The model is evaluated by how well the model predicts held out data (data that was not used during the training of the model). However, neither of these uses seems to parallel the use of predict in philosophy of science where the emphasis is on the prediction being novel, i.e., something that hasn’t been observed yet.

Confusingly, the word explain is also used in the context of statistical hypothesis testing. The statistical measure R-squared (R2) is the proportion of variance in one variable that is explained by another in a linear regression. This use of the word explain in statistical hypothesis testing is distinct from scientific explanation, but the two are sometimes not clearly distinguished in scientific writing. For example, consider this motivating statement for the Algonauts project, whose 2019 edition is dedicated to “Explaining the Human Visual Brain”:

Currently, particular deep neural networks trained with the engineering goal to recognize objects in images do best in accounting for brain activity during visual object recognition (Schrimpf et al., 2018; Bashivan, Kar, & DiCarlo, 2019). However, a large portion of the signal measured in the brain remains unexplained. This is so because we do not have models that capture the mechanisms of the human brain well enough. Thus, what is needed are advances in computational modelling to better explain brain activity (Cichy et al., 2019).

When discussing unexplained signals, the authors allude to statistical explanation while talk of capturing neural mechanisms hints to scientific explanation. When in reality, this project is about evaluating models based on their ability to predict (in the machine learning sense) neural activity. When they lament that a “large portion of the signal measured in the brain remains unexplained”, they invoke the notion of explained variance. Rather than trying to develop a scientific explanation for a phenomenon of interest, they are concerned with statistically explaining, or in this case, being able to predict, the variance in the collected data—variance which may or may not be causally related to any number of different neural or cognitive phenomena.

Many of the issues described above can be subsumed under the notion of generalization. The philosopher’s term accommodation does not imply any generalization beyond the observations used during the construction of the theory (or training of the model). The typical notion of generalization in psychology is akin to within-distribution generalization in machine learning. One assumes (or tries to ensure) that their sample of subjects represents a random sample from a population. The goal of statistical inference is to make general statements about the population from the measurements made on a sample. The notion of novel prediction in philosophy of science could be seen as an example of out-of-distribution generalization in machine learning.

The goal to explain as much variance as possible or to predict as accurately as possible expresses a desire for completeness. Philosophers of scientific explanation warn against over-completeness.

It is important to note, in this connection, that particular [explananda] do not necessarily embody all of the features of the phenomena which are involved. For example, archaeologists are attempting to explain the presence of a particular worked bone at a site in Alaska. The relevant feature of the explanandum are the fact that the bone is thirty thousand years old, the fact that it was worked by a human artisan, and the fact that it has been deposited in an Alaskan site. Many other features are irrelevant to this sought-after explanation. The orientation of the bone with respect to the cardinal points of the compass at the time it was discovered, its precise size and shape (beyond the fact that it was worked), and the distance of the site from the nearest stream are all irrelevant. It is important to realize that we cannot aspire to explain particular phenomena in their full particularity. . . . In explanations of particular phenomena, the explanation-seeking why-question—suitably clarified and reformulated if necessary—should indicate those aspects of the phenomena for which an explanation is sought. (Salmon, 1984, pg.273-4)

The project of collecting large-scale neural datasets and building models that explain as much variance as possible in that data is one of mere description rather than explanation. Descriptive science is unambiguously crucially important to scientific progress. Recall the first aspect of Craver’s notion of mechanical explanations is characterization of the phenomenon to be explained. However, the distinction between explanation and mere description is still important. Specific why-questions may eventually be motivated by such descriptive characterizations, but only if we don’t mistake them for explanations prematurely.

General Conclusions

Comparing activations in biological and artificial neural networks is a promising approach to study the architectures and learning procedures that support brain-like representations and the nature of representations in intelligent systems. However, this scientific project is not just about chasing high accuracy. As much as one might like to, the scientific problems posed in neuroscience cannot be reformulated as engineering problems. The (long term) goal of science is to generate scientific explanations, which is not the same as statistically explaining the variance in our data. At this particular moment in computational neuroscience, there is a high degree of uncertainty about what such explanations might look like for many phenomena of interest. Therefore, the field may benefit from a closer relationship with philosophers of neuroscience concerned with scientific explanation. Philosophy of science offers conceptual scaffolds that can help refine a vision of an integrated science of intelligence.

Part of the value of deep learning from a neuroscience perspective could come from the fact that deep learning is theory-poor compared to other areas of machine learning. That there are a lot of open questions in deep learning theory may reflect generic challenges of studying learning in distributed networks. This positions deep learning science as a model science for neuroscience. The methods and concepts that prove useful for explaining phenomena in deep learning may inspire new methods and ways of thinking in neuroscience, due to the similar scientific problems posed in these two fields and the relatively ease with which artificial systems can be analyzed compared to their biological counterparts. In this way, the opportunities for transfer between deep learning and neuroscience span several scientific and meta-scientific levels.

The arguments presented here are not intended to advocate for a deep learning approach to neuroscience over other approaches. The purpose of the arguments presented is to justify and clarify the merits of a deep learning approach to neuroscience as one among many. The addition of a deep learning approach increasing the epistemic diversity of the set approaches employed. Innovative and diverse approaches in an epistemically humble research community will better lead us towards truth.

Bibliography

  • Alain, G. and Bengio, Y. (2016). Understanding intermediate layers using linear classifier probes. arXiv, page 1610.01644v3.
  • Bahdanau, D., Murty, S., Noukhovitch, M., Nguyen, T. H., de Vries, H., and Courville, A. (2018). Systematic Generalization: What Is Required and Can It Be Learned? pages 1–16.
  • Bashivan, P., Kar, K., and DiCarlo, J. J. (2019). Neural population control via deep image synthesis. Science, 364(6439).
  • Bengio, Y., Lee, D.-h., Bornschein, J., and Lin, Z. (2014). Towards Biologically Plausible Deep Learning.
  • Brette, R. (2019). Neural coding : the bureaucratic model of the brain.
  • Cadena, S. A., Sinz, F. H., Muhammad, T., Froudarakis, E., Cobos, E., Walke, E. Y., Reimer, J., Bethge, M., Tolias, A. S., and Ecker, A. S. (2019). How well do deep neural networks trained on object recognition characterize the mouse visual system? In Real Neurons & Hidden Units NeurIPS Workshop.
  • Chemero, A. (2009). Radical Embodied Cognitive Science. The MIT Press, Cambridge, MA. Cichy, R. M., Roig, G., Andonian, A., Dwivedi, K., Lahner, B., Lascelles, A., Mohsenzadeh,
  • Y., Ramakrishnan, K., and Oliva, A. (2019). The Algonauts Project: A Platform for Com- munication between the Science of Biological and Artificial Intelligence. In Computational Cognitive Neuroscience.
  • Devezer, B., Nardin, L. G., Baumgaertner, B., and Buzbas, E. O. (2019). Scientific discovery in a model-centric framework: Reproducibility, innovation, and epistemic diversity. PLoS ONE, 14(5):1–23.
  • Diedrichsen, J. and Kriegeskorte, N. (2017). Representational models: A common framework for understanding encoding, pattern-component, and representational-similarity analysis. PLoS Computational Biology, 13(4).
  • Elsayed, G. F., Shankar, S., Cheung, B., Papernot, N., Kurakin, A., Goodfellow, I., and Sohl-Dickstein, J. (2018). Adversarial Examples that Fool both Human and Computer Vision.
  • Gelder, T. v. (1998). The Dynamical Hypothesis in Cognitive Science. Behavioural and Brain Sciences, 21:615–665.
  • Gerven, M. v. and Bohte, S. (2017). Editorial: Artificial Neural Networks as Models of Neural Information Processing. Front. Comput. Neurosci., 11(114).
  • Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Explaining and harnessing adversarial examples. In 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings.
  • Goyal, A., Lamb, A., Hoffmann, J., Sodhani, S., Levine, S., Bengio, Y., and Schölkopf, B. (2019). Recurrent Independent Mechanisms.
  • Guerguiev, J., Lillicrap, T. P., and Richards, B. A. (2017). Towards deep learning with segregated dendrites. eLife, 6(e22901).
  • Jonas, E. and Kording, K. P. (2017). Could a Neuroscientist Understand a Microprocessor? PLoS Computational Biology, 13(1).
  • Kell, A. J. and McDermott, J. H. (2019). Deep neural network models of sensory systems: windows onto the role of task constraints. Current Opinion in Neurobiology, 55:121–132.
  • Lillicrap, T. P., Cownden, D., Tweed, D. B., and Akerman, C. J. (2014). Random feedback weights support learning in deep neural networks. page 14.
  • Lillicrap, T. P. and Kording, K. P. (2019). What does it mean to understand a neural network? (July):1–9.
  • Lindsay, G., Moskovitz, T., Yang, G. R., and Miller, K. (2019). Do Biologically-Realistic Recurrent Architectures Produce Biologically-Realistic Models? pages 779–782.
  • Lindsay, G. W. and Miller, K. D. (2018). How biological attention mechanisms improve task performance in a large-scale visual system model. eLife, 7:1–29.
  • Love, B. C. (2019). Levels of Biological Plausibility. PsyArXiv Preprints.
  • Marcus, G. (2018). Deep Learning: A Critical Appraisal.
  • Marder, E. (2015). Understanding Brains: Details, Intuition, and Big Data. PLoS Biology, 13(5):1–6.
  • Marr, D. and Nishihara, H. K. (1978). Representation and recognition of the spatial or- ganization of three dimensional shapes. Proceedings of the Royal Society of London B: Biological Sciences, 200(1140):269–294.
  • Mehrer, J., Spoerer, C. J., Kriegeskorte, N., and Kietzmann, T. C. (2020). Individual differences among deep neural network models.
  • Olah, C., Satyanarayan, A., Johnson, I., Carter, S., Schubert, L., Ye, K., and Mordvintsev, A. (2018). The Building Blocks of Interpretability.
  • Ponce, C. R., Xiao, W., Schade, P. F., Hartmann, T. S., Kreiman, G., and Livingstone, M. S. (2019). Evolving Images for Visual Neurons Using a Deep Generative Network Reveals Coding Principles and Neuronal Preferences. Cell, 177(4):999–1009.
  • Raghu, M., Gilmer, J., Yosinski, J., and Sohl-Dickstein, J. (2017). SVCCA: Singular Vector Canonical Correlation Analysis for Deep Understanding and Improvement. NeurIPS.
  • Richards, B. A., Lillicrap, T. P., Beaudoin, P., Bengio, Y., Bogacz, R., Christensen, A., Clopath, C., Costa, R. P., de Berker, A., Ganguli, S., Gillon, C. J., Hafner, D., Kepecs, A., Kriegeskorte, N., Latham, P., Lindsay, G. W., Miller, K. D., Naud, R., Pack, C. C., Poirazi, P., Roelfsema, P., Sacramento, J., Saxe, A., Scellier, B., Schapiro, A. C., Senn, W., Wayne, G., Yamins, D., Zenke, F., Zylberberg, J., Therien, D., and Kording, K. P. (2019). A deep learning framework for neuroscience. Nature Neuroscience, 22(11):1761–1770.
  • Salmon, W. C. (1984). Scientific explanation and the causal structure of the world. Princeton University Press.
  • Santoro, A., Raposo, D., Barrett, D. G., Malinowski, M., Pascanu, R., Battaglia, P., and Lillicrap, T. (2017). A simple neural network module for relational reasoning. Advances in Neural Information Processing Systems, 2017-Decem(Nips):4968–4977.
  • Schölkopf, B. (2019). Causality for Machine Learning. pages 1–20.
  • Storrs, K. R. and Kriegeskorte, N. (2020). Deep Learning for Cognitive Neuroscience. In
  • Poeppel, D., Mangun, G. R., and Gazzaniga, M. S., editors, The Cognitive Neurosciences. MIT Press, 6th edition.
  • Xu, Y. (2020). Limited correspondence in visual representation between the human brain and convolutional neural networks.
  • Zador, A. M. (2019). A critique of pure learning and what artificial neural networks can learn from animal brains. Nature Communications, 10(3770).